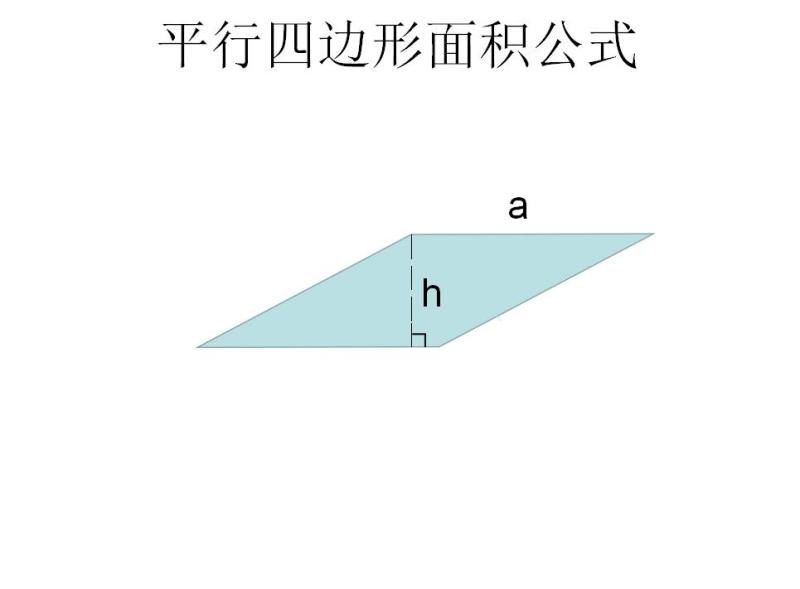
扇形の半径を求めるときも、面積の公式または弧の長さの公式を利用します。 公式にわかっている値を代入して、「 \(\text{(半径)} = \) 〜 」の形に書き換えていけばいいだけです! 実際に例題を見てみましょう。 例題①「面積がわかっている場合」弧度法で扇の弧の長さと面積を求める公式 弧度法を使って、扇の弧の長さと面積を求める公式を紹介します。 半径がr、中心角がθの扇の弧の長さを"l"、面積を"S"とするとき ※θは、度数法ではなく弧度法三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)

扇形面积公式 搜索结果 哔哩哔哩弹幕视频网 つロ乾杯 Bilibili
扇面積 公式
扇面積 公式-この公式が使える問題はさほど出題されませんが,運良く巡り合えれば相当な時間短縮になります。 極座標の面積公式を用いる例,公式の証明,諸注意を整理しました。 極方程式の面積公式の使用例1 まずは一番簡単な例である円の面積を求めてみます。Part 2 Part 2扇(おうぎ)形の面積を求める公式3つと弧の長さの求め方をお伝えします。 面積と弧の長さは比例ですべて解けるのですがこれを苦手にしている中学生はものすごく多いです。 これには当然とも言える理由が3つあります。



探究圆的弧长扇形面积公式教案模板 探究圆的弧长扇形面积公式教案文档下载 文档铺 精选精华文档资源 助您学习工作更轻松
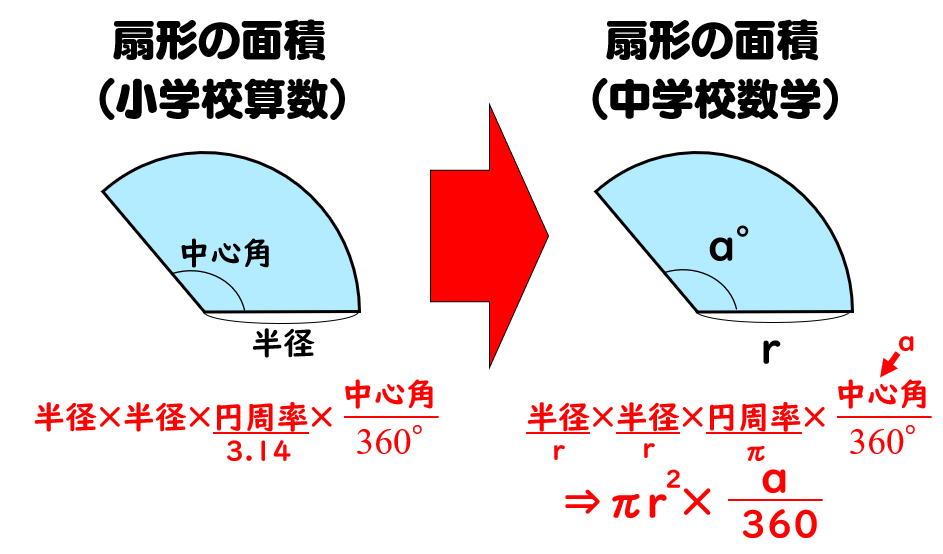
中1数学 中学数学3分で簡単にわかる!「扇形(おうぎ形)の面積の求め方」の公式 中1数学 中学数学速さの単位変換・換算の2つの方法V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jinScipursuit 面積の求め方 扇形 扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 また、2行目の l は扇形の弧の長さを表します。 このページの続きでは、この 公式の導き方 と、 扇形の面積を求める計算問題
図形で使う公式・定理の一覧 扇の孤の長さ"l" 扇の半径をr、中心角をx、孤の長さをlとしたとき 扇の面積"s" 扇の半径をr、中心角をx、面積をSとしたとき 角柱の体積"v数学Aの平面図形で使う定理の一覧 三角形の角の二等分線と辺の比 三角形ABCにおいて、∠BACを二等分する弧の長さがわかっている時、扇型の面積は、(弧の長さ)×(半径)÷2 という公式で求めることが出来ます。 どうして この式で面積を求めることが出来るか?を小学生向けに図解を含めて解説します。中1数学 中学数学3分で簡単にわかる!「扇形(おうぎ形)の面積の求め方」の公式 中1数学 中学数学速さの単位変換・換算の2つの方法
No003 扇形の面積と円弧の長さ 扇形の面積 A m 2 扇形の角度 θ ° 扇の半径 r m 扇形の面積 A m 2 扇形の角度 θ rad 扇の半径 r m 円弧の長さ l m 扇形の角度 θ ° 扇の半径 r m図形で使う公式・定理の一覧 扇の孤の長さ"l" 扇の半径をr、中心角をx、孤の長さをlとしたとき 扇の面積"s" 扇の半径をr、中心角をx、面積をSとしたとき 角柱の体積"v数学Aの平面図形で使う定理の一覧 三角形の角の二等分線と辺の比 三角形ABCにおいて、∠BACを二等分するはじめに 半径が「r」、中心角が「θ」である扇の面積「S」は で求めることができました。 ここでは、 中心角「θ」が与えられていない その代わりに弧の長さ「l」は与えられている 場合に扇の面積を求める公式を紹介しましょう。 半径「r


1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆面积s的360分之 扇形的面积公式 1 设圆的半径为r圆心角为n度 那么扇形面积s扇形是圆 面积s的360分之 扇形的面积公式为 S 作业 慧海网



九年级数学下册24 7 弧长与扇形的面积教案 新版 沪科版下载 Word模板 爱问共享资料
三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから)扇形面積=円の面積×( 扇の内角/360°) 三角形の面積=( 半径 2 ×sin扇の内角 )/2 ・・・二辺夾角法 扇の面積-三角形の面積=円弧の面積 WingneoのIAの計算方法 円弧の始点・終点2点の座標値を丸める。「円弧面積の弦長を求める為の座標丸め」考え方は弧の長さと同様。 完全な円の面積( πr2 π r 2 )と比べて、扇形の割合をかけた値が扇形の面積になります。 『半径×半径×314× 中心角 360 × 314 × 中 心 角 360 』⇒『πr2 × a 360 π r 2 × a 360 』 5扇形の面積の公式(弧の長さからの導出)



积分扇形面积公式 三人行教育网 Www 3rxing Org


弧长公式及扇形面积公式设扇形的弧长为l 圆心角为a 弧度 半径为r 则l S扇 作业 慧海网
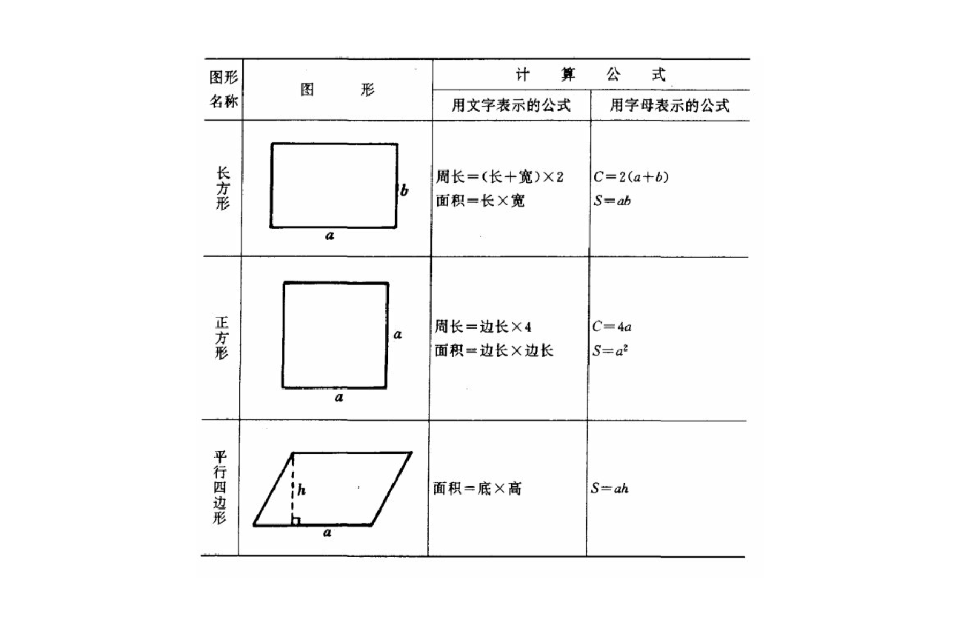
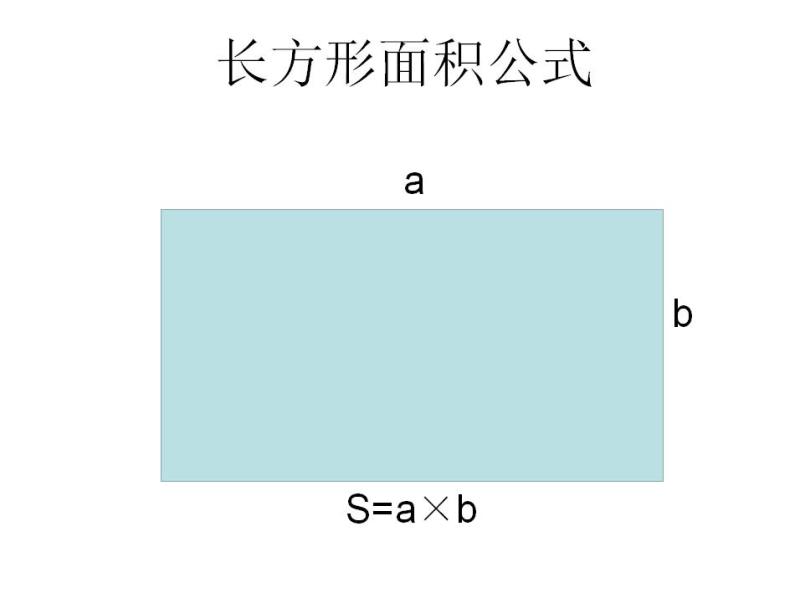
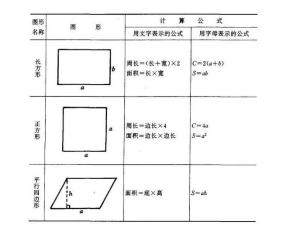
$$(円の面積)×\frac{1}{3}=(おうぎ形の面積)$$ $$(円周)×\frac{1}{3}=(弧の長さ)$$ となるのです。 解答 面積は, $$\pi×3^2×\frac{1}{3}=\underline{3\pi(cm^2)}(答え)$$ 弧の長さは, $$2\pi×3×\frac{1}{3}=\underline{2\pi(cm)}(答え)$$ 映像授業による解説 動画はこちら 4>孤の長さと面積がわかっていて、半径をxとするとどんな方程式になりますか? 教えてください まずは弧の長さと半径から中心角を計算しよう。 直径x円周率x中心角÷360 = 弧の長さ だね。そのあとに扇型の面積の公式で計算するんだ求積公式(平面) a=面積 正方形 長方形 平行四辺形 備考 a寸法はb辺に対し直角に測ったもの 直角三角形 a=面積 鋭角三角形 鈍角三角形 台 形 不平行四辺形 円 a=面積 円分 欠 円 環 形 扇 形



すごい扇面積公式 壁紙配布



扇形的面积公式 你搜我答
扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度(単位はラジアン) 公式を用いて、例題の扇形の面積を求めましょう。角度60°の扇形があります。半径が6です。面積を求めてください。次の図のように,1辺の長さがa(cm)の正方形ABCDを頂点Bを中心として45°回転したとき,辺ADが通過する部分の面積(cm 2) ヒント 上の問題4の結果(問題の図は上の左側)から,次の図の黄色で示した図形の面積を引くとよい.扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度(単位はラジアン) 公式を用いて、例題の扇形の面積を求めましょう。角度60°の扇形があります。半径が6です。面積を求めてください。



例題 扇形的面積計算 六年級 圓面積與扇形面積 均一教育平台


私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院
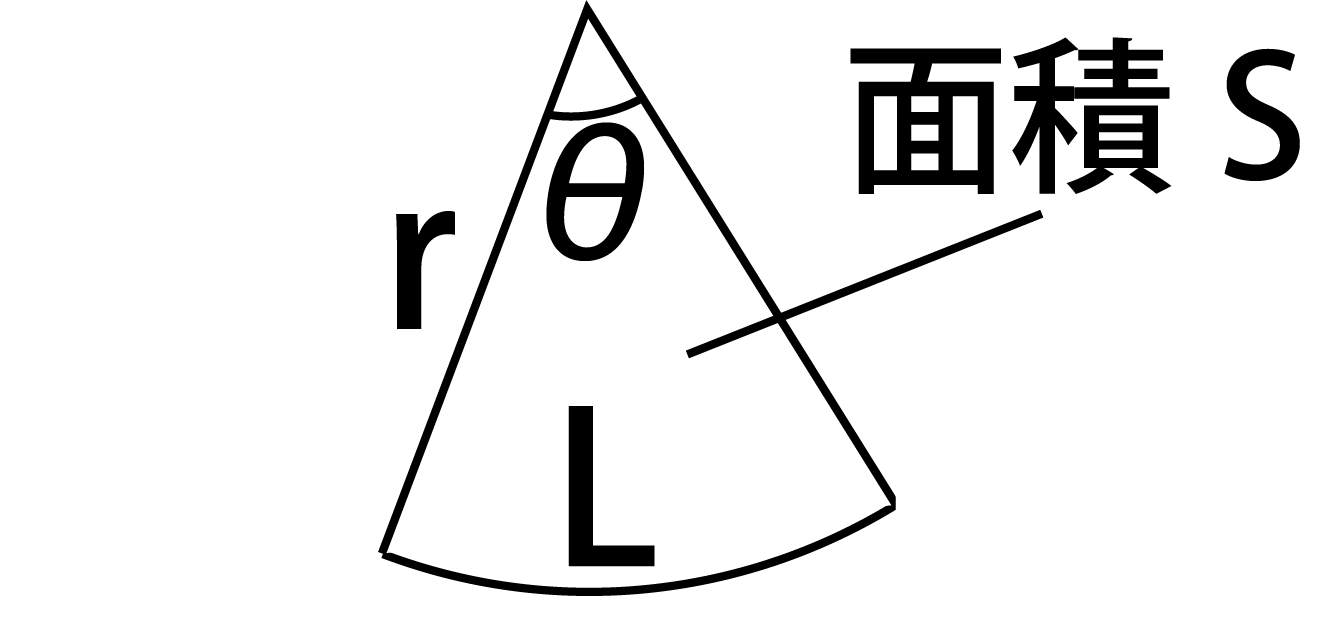
>孤の長さと面積がわかっていて、半径をxとするとどんな方程式になりますか? 教えてください まずは弧の長さと半径から中心角を計算しよう。 直径x円周率x中心角÷360 = 弧の長さ だね。そのあとに扇型の面積の公式で計算するんだV = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin"扇形の弧の長さと面積"の公式とその証明です! 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l=rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証



如何用几何画板验证圆面积公式 教育频道 手机搜狐



计算扇形和扇环的面积用扇形面积公式推导扇环面积的过程
《参考》 1)三角形の面積と重心 2)扇型の面積と重心 3)角錐台の体積と重心 rまとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった? ? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360 「円とおうぎ形」がテストにでるときに確認したいね^^ おうぎ形の面積をマスターしたら次は おうぎ形の中心角 を求めてみよう! Qikeru:学びを楽しくわかりやすく 1 user2 θ b a ( b − a) cos 2 θ) r ( θ) 2 = a 2 b 2 b 2 cos 2 θ a 2 sin 2 θ ( 2) e l l i p t i c a l a r c h L = a E ( x ( θ 0) a, k) − a E ( x ( θ 1) a, k) x ( θ) = r ( θ) cos θ, k = 1 − ( b a) 2, a ≥ b, π 2 ≥ θ ≥ 0 E ( x, k) 2 n d i n c o m p l e t e e l l i p t i c i n t e g r a l


数学中扇形的面积公式是什么 初三网


扇形面积公式小学 初三网
No003 扇形の面積と円弧の長さ 扇形の面積 A m 2 扇形の角度 θ ° 扇の半径 r m 扇形の面積 A m 2 扇形の角度 θ rad 扇の半径 r m 円弧の長さ l m 扇形の角度 θ ° 扇の半径 r m


计算扇形面积公式有哪些如何计算 高三网



扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积



扇形面积 扇形面积的公式是什么 扇形面积公式大全 扇形面积公式小学



壁纸资源网



すごい扇面積公式 壁紙配布



扇形周長與面積 6年級數學 Grade 6 Math Fan Shaped Area Youtube



扇形面积公式和图解 第1页 一起扣扣网


面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書



99以上扇面積公式 壁紙引用画像hd



圆台面积公式的推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客


扇形面积公式 腾讯视频


公式扇形面积公式 扇形侧面积 扇形的公式 扇形周长公式



扇形面積 扇形是與圓形有關的一種重要圖形 其面積與圓心角 頂角 圓半徑 圓 華人百科


数理天地


功課幫


扇形面积公式弧长公式 高三网



探究圆的弧长扇形面积公式教案模板 探究圆的弧长扇形面积公式教案文档下载 文档铺 精选精华文档资源 助您学习工作更轻松



初中数学有关圆的计算问题 注意选用合理的公式才能避免出错 每日头条



すごい扇面積公式 壁紙配布


扇形面积公式及计算扇形面积计算带图


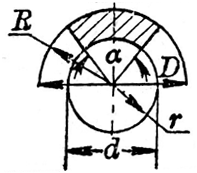
扇环形面积计算公式 三人行教育网 Www 3rxing Org


扇形 扇环 三角形 圆面积 弓形 椭圆面积公式圆面积计算器 爱华网



拱形面积计算公式图解 第1页 一起扣扣网


扇形面积公式 腾讯视频



扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积


面积公式 搜狗百科



面積公式 面積公式包括扇形面積公式 圓形面積公式 弓形面積公式 菱形面 百科知識中文網


課堂實錄 扇形面積 六上 雪花新闻



老师 弧长和扇形面积所有公式的每个字母代表的意思的是什么啊 我老是搞混 360问答


扇形面积公式是什么弧长公式和扇形面积公式是什么



不喜歡數學幹嘛學編程呢 C語言小程序 圓台表面積公式推導 每日頭條


扇环面积计算器 计算专家



すごい扇面積公式 壁紙配布
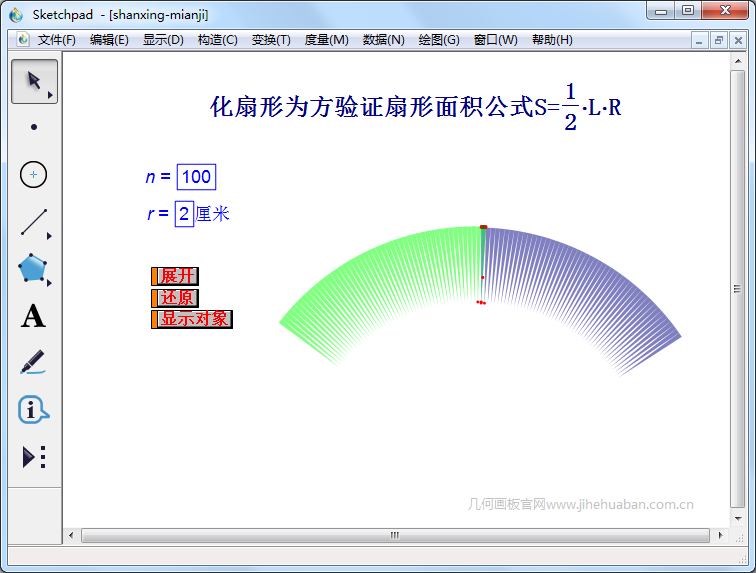


扇形面积公式 这样验证起来秒懂 Weixin 的博客 Csdn博客 扇形面积公式



扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积


面积公式 搜狗百科


面积公式 搜狗百科



扇形面積公式 公式 推導過程 注意事項 中文百科全書


扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积



扇形面積為何如此計算呢 Isdp08am 隨意窩xuite日誌



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



初中數學 圓的性質 扇形面積公式及應用 異常重要 每日頭條



扇形弧长公式图片 第1页 一起扣扣网


空间几何积 图文 百度文库



锥形展开图面积公式 第1页 一起扣扣网


扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积


私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院
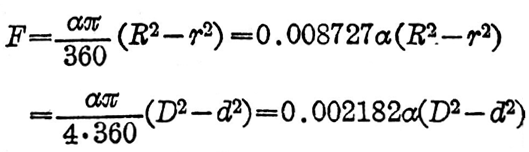


扇环面积计算器 计算专家


三角形面积公式 腾讯视频
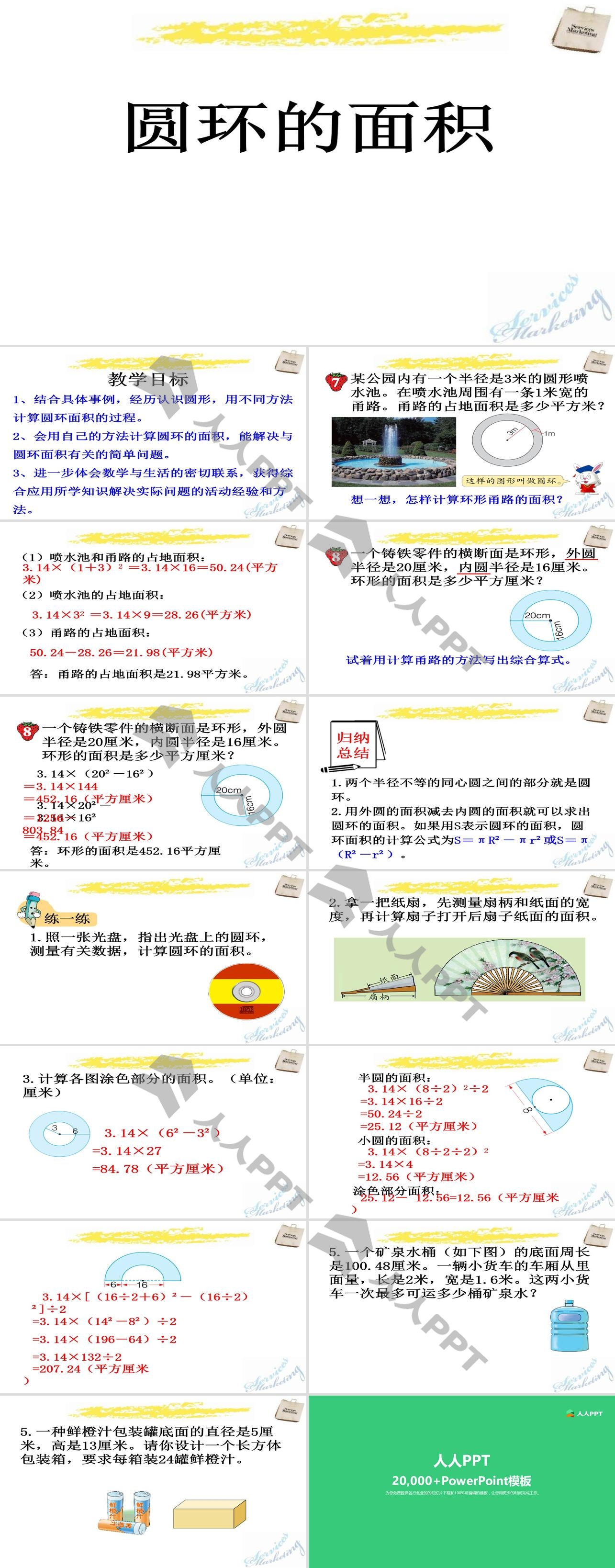


圆环的面积 圆的周长和面积ppt课件 Ppt课件下载 人人ppt


高中数学易错点 重难点系列之 巧记空间几何体的面积和体积公式



扇环面积计算公式图解 第1页 图说健康



扇形的圆心角的取值范围 三人行教育网 Www 3rxing Org



面積公式 面積公式包括扇形面積共式 圓形面積公式 弓形面積公式 菱形面積公 華人百科



面积公式 搜狗百科
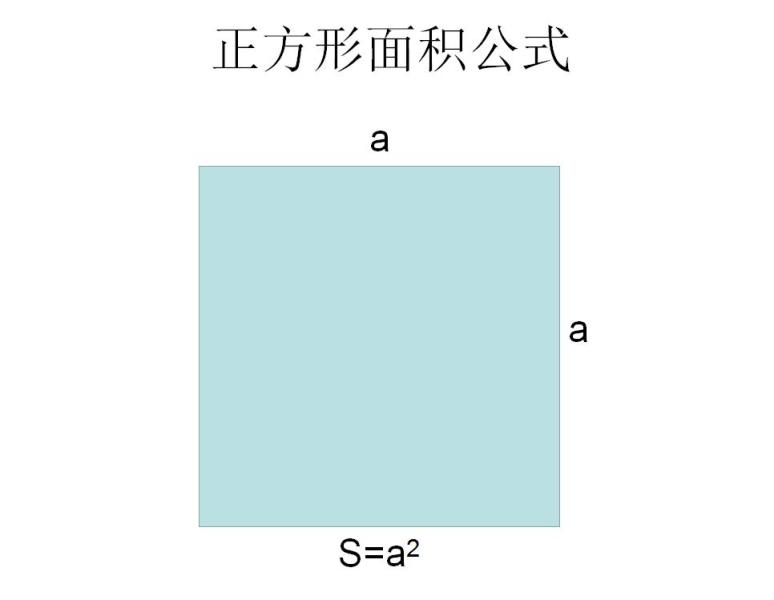


面积公式 搜狗百科


弧的周长面积计算公式 学习岛



扇形公式大全 扇形面积怎么算 扇形面积公式大全 求扇形的面积



如何计算圆的面积 知识库 February 21



圆锥角度计算公式图解 第1页 一起扣扣网


扇形面积 扇形面积 头条百科



扇形面积公式 搜索结果 哔哩哔哩弹幕视频网 つロ乾杯 Bilibili



中考有关圆的计算用下载 Word模板 爱问共享资料


私校資優數學 面積題目 扇葉形狀 Nova的科學反主流學院
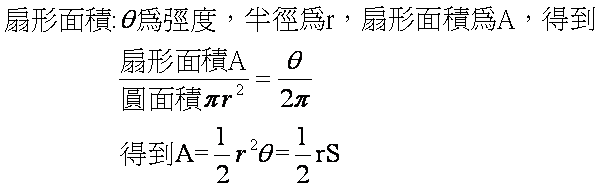


扇形的弧長與面積


锥台面积公式扇形面积的公式 锥形面积的公式 锥形台的面积公式



扇形周长计算公式汉字



扇环面积计算公式图解 第1页 一起扣扣网


扇环周长计算公式图解 第1页 要无忧健康图库



360影视 影视搜索


扇形面积公式扇形面积计算公式 天奇生活



高中数学易错点 重难点系列之 巧记空间几何体的面积和体积公式 每日头条


圆的截面积的公式是什么 日博开户 Www B Com


求扇形的面积和周长的文字公式及字母公式 香蕉皮作业网



扇形の面積の求め方 公式と計算例
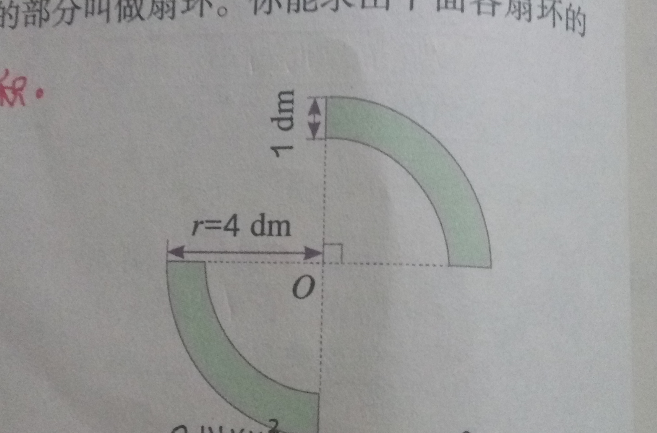


扇環 扇環 扇環的面積 大扇形的面積減小扇形的面積 圓台展開扇環的半徑 相關公式 中文百科全書



球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com


課堂實錄 扇形面積 六上 雪花新闻



すごい扇面積公式 壁紙配布


扇环周长计算公式图解 第1页 要无忧健康图库



圓的周長與面積 27 扇形的複合圖行計算2 Youtube



扇形的面积公式是多少 数学理工学科



Ppt 教學分享 六年級下學期數學領域 圓面積powerpoint Presentation Id



扇环面积计算公式图解 第1页 图说健康



日行一 扇 扇形面積與周長的公式 Youtube


椭圆扇面面积公式本人知道椭圆形面积公式 3 14 A B但不知道椭圆扇面积该如何计算 有那位高手知道椭圆扇形面积公式请指



0 件のコメント:
コメントを投稿